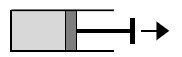Bryła sztywna

Moment bezwładności walca=  ½ mr², kuli= 2/5 mr² , pręta= 1/12 ml²

Zad.1. Wyznacz moment bezwładności bryły pokazanej na rysunku. Przyjmij R = 20 cm, masę kuli 0,5 kg.

Masa walca jest 2 razy większa od masy kuli. Pomiń masę pręta.

 Zad. 2. Oblicz prędkość i przyspieszenie walca staczającego się z równi, jeśli kąt jej nachyl.  wynosi 45⁰, a wysokość 0,9m. Jak długo trwał ruch walca po równi? M = 400g, r = 10 cm.

 Zad.3. Moment siły F (na rys.) względem osi obrotu wynosi 40 Nm. Ile wynosi siła F? Dorysuj moment siły na rys.

Zad. 4. Koło zamachowe o momencie bezwładności I = 0,2 kgm² obraca się wokół poziomej osi przechodzącej przez jego środek, wykonując n = 600 obr/min. Przy hamowaniu koło zatrzymuje się po upływie czasu Δt = 20 s. Oblicz moment siły hamującej.

Zad. 5.  Dwa walce połączone ze sobą (jak na rys.) wirowały z prędkością 20 1/s. W trakcie wirowania dolny walec odpadł od górnego.  Z jaką prędkością wiruje teraz górny walec? Przyjmij jednakowe masy walców, r = ½ R.

6. Oblicz stosunek energii kinetycznej ruchu obrotowego do postępowego dla kuli toczącej się bez poślizgu po równi pochyłej.

a) jakie będzie przyspieszenie kuli przy staczaniu się z równi o kącie nachylenia 45⁰

7. Oblicz moment bezwładności układu kul o promieniach R i masach m według rysunku

8. Oblicz siły nacisku belki na punkty podparcia, jeżeli masa belki wynosi 100 kg, jej długość 4 m, co przedstawia rysunek:

INNE Zadania

 zad.1 . a) Oblicz stosunek energii kinetycznej ruchu obrotowego do postępowego dla kuli toczącej się bez poślizgu po równi pochyłej.

b) jakie będzie przyspieszenie kuli przy staczaniu się z równi o kącie nachylenia 45 stopni

zad.2 Oblicz moment bezwładności układu kul o promieniach R i masach m według rysunku:

zad.3 Oblicz siły nacisku belki na punkty podparcia, jeżeli masa belki wynosi 100 kg, jej długość 4 m, co przedstawia rysunek:

zad.4. Koło zamachowe o momencie bezwładności I = 0,2 kgm2 obraca się wokół poziomej osi przechodzącej przez jego środek, wykonując n = 600 obr/min. Przy hamowaniu koło zatrzymuje się po upływie czasu Δt = 20 s. Znajdź moment siły hamującej i liczbę obrotów do chwili zatrzymania.
odp: M = 0,2π Nm, N=100 obr.
zad.5. Na rurę o cienkich ściankach nawinięto nić, której wolny koniec przymocowano do sufitu. Rura odkręca się z nici pod działaniem własnego ciężaru (rys.). Znajdź przyspieszenie rury i siłę napięcia nici, jeżeli masę i grubość nici można zaniedbać. Początkowa długość nici jest dużo większa od promienia rury. Ciężar rury wynosi Q.

zad.6. Przez bloczek zawieszony na poziomej osi przerzucono nieważką i nierozciągliwą nić, do końców której przymocowano ciężarki o masach m1 = 0,5 kg i m2 = 0,2 kg. Masa bloczka wynosi m = 0,4 kg. Bloczek traktujemy jako jednorodny krążek. Znajdź liniowe przyspieszenie ciężarków. Przyjmij, że nić nie ślizga się po bloczku.
zad.7 Z równi pochyłej o kącie nachylenia α stacza się bez poślizgu ciało o momencie bezwładności I, masie m i promieniu r. Wyznacz jego przyspieszenie liniowe, kątowe i siłę tarcia.
zad.8. Pełne, jednorodne ciała: walec i kula staczają się bez poślizgu z równi pochyłej o kącie nachylenia α i wysokości h. Masy i promienie tych ciał są jednakowe. Które z nich stoczy się wcześniej?
zad.9. Kula o początkowej prędkości w ruchu postępowym v0 = 10 m/s wtacza się bez poślizgu na równię pochyłą o kącie nachylenia 45 st. Jaką drogę przebędzie kula po równi do chwili zatrzymania się i po jakim czasie wróci do podstawy równi?

zad.10. Środek masy kuli bilardowej posiada początkową prędkość v0. Promień kuli wynosi R, jej masa M, a współczynnik tarcia pomiędzy kulą i stołem jest równy µ. Jak daleko przesunie się kula po stole, zanim przestanie się ślizgać?

zad.11. W czasie pokazów gimnastyki artystycznej można oglądać ćwiczenie, w którym obręcz rzucona przez zawodniczkę tocząc się początkowo z poślizgiem wraca ku niej i w końcowej fazie ruchu toczy się już bez poślizgu. Jest to możliwe, jeżeli w czasie rzutu zawodniczka nada obręczy ruch obrotowy o odpowiednim kierunku. Znajdź związek pomiędzy początkową wartością prędkości ruchu postępowego v0 i prędkości kątowej ω0.
zad.12. Po idealnie gładkiej poziomej powierzchni ślizga się bez obrotów walec. Prędkość liniowa środka masy wynosi v0, a kierunek prędkości jest prostopadły do osi walca. W pewnej chwili powierzchnia pod walcem staje się szorstka, a współczynnik tarcia posuwistego przyjmuje wartość f. Po jakim czasie walec będzie się toczył bez poślizgu i jaka będzie wtedy prędkość jego środka masy?
zad.13. Kołowrót o masie m, momencie bezwładności I0 i promieniach zewnętrznym R oraz wewnętrznym r leży na płaszczyźnie poziomej (rys.). Na kołowrót nawinięta jest nić, do której przyłożono siłę F. Opisz ruch kołowrotu w zależności od kąta α jaki tworzy nić z kierunkiem poziomym.

zad.14. Ciężki walec o promieniu R i momencie bezwładności I0 wiruje z prędkością kątową ω0. W chwili t = 0 do dźwigni hamulcowej przyłożono siłę F (rys.) wskutek czego walec zatrzymuje się po czasie t. Ramiona dźwigni mają długości l1 i l2, a współczynnik tarcia między dźwignią i walcem wynosi f. Oblicz wartość siły F.

zad.15 * Walec o masie M i promieniu r może toczyć się po poziomym stole. Na walec nawinięta jest nieważka i nierozciągliwa nić, którą przerzucono przez nieważki bloczek. Na końcu nici zawieszono ciężarek o masie m (rys. ). Wyznacz przyspieszenie ciężarka i siłę tarcia działającą na walec przyjmując, że może być on pełen lub wydrążony (cienkościenna rura).

zad.16. Na krześle mogącym obracać się swobodnie wokół osi pionowej siedzi student i trzyma w wyprostowanych rękach odważniki po m = 5 kg każdy. Odległość każdego odważnika od osi obrotu wynosi l1 = 80 cm. Krzesło wiruje wykonując n1 = 1 obr/sek. Jak zmieni się szybkość wirowania studenta, jeśli zegnie on ręce tak, że odważniki będą w odległości l2 = 20 cm od osi obrotu? Moment bezwładności studenta i krzesła (całkowity) względem osi obrotu wynosi I0 = 3 kgm2.
zad.17.* Belka o długości l i masie M może swobodnie obracać się wokół poziomej osi przechodzącej przez jeden z jej końców. W drugi koniec belki uderza kula o masie m mająca poziomą prędkość v0 (rys.). Kula grzęźnie w belce. Znajdź prędkość kątową belki tuż po uderzeniu kuli. W jakie miejsce belki powinna uderzyć kula, aby składowa pozioma siły reakcji osi w chwili uderzenia wynosiła zero?

zad.18.* Na brzegu poziomej, okrągłej platformy o masie M i promieniu R stoi student o masie m. Platforma może obracać się bez tarcia wokół pionowej osi. Jaka będzie prędkość kątowa platformy ω, jeżeli student zacznie chodzić wzdłuż jej brzegu ze stałą względem niej prędkością v. Jaką drogę przebędzie student względem platformy w czasie jej jednego pełnego obrotu?
zad.19.* Samolot sportowy z jednym śmigłem lecący z prędkością v = 360 km/h wykonuje zakręt o promieniu r = 800 m. Oblicz moment sił wywierany przez śmigło na samolot, jeżeli moment bezwładności śmigła wykonującego n = 2400 obr/min wynosi I = 15 kgm2.
zad.20. Dane są dwie pełne kule A i B wykonane z tego samego materiału. Masa kuli A jest 8 razy większa od masy kuli B. Ile razy moment bezwładności kuli A jest większy od momentu bezwładności kuli B ? Moment bezwładności kuli I = 0,4mr2.

termodynamika

 TEORIA

1. Podaj cechy gazu doskonałego. Równanie gazu doskonałego. Zasady termodynamiki
2. Omów przemianę izotermiczną, izobaryczną, izochoryczną, adiabatyczną
- przedstaw na wykresie zależności p(V), p(T), V(T) w tej przemianie
- podaj zależności fizyczne między parametrami gazu w tej przemianie (równanie gazu doskonałego)
3. Narysuj cykl przemian silnika Carnota i nazwij je

ZADANIA:
zad. 1 W butli o pojemności 50l znajduje się tlen. Temp. początkowa wynosi 280 K, a ciśnienie 100 kPa. Butla na słońcu nagrzała się do temp. 430 K, a ciśnienie  wyniosło 120 kPa.   Oblicz liczbę moli, Tk oraz ciepło dostarczone przez słońce.

zad 2.

W naczyniu znajdował się gaz pod ciśnieniem 2·105 Pa i o temperaturze 25 °C, zamknięty tłokiem o powierzchni przekroju 50 cm2. Początkowo objętość gazu wynosiła 1000 cm3, a następnie przesunięto tłok o 5 cm w prawo, jak pokazano na rysunku. Temperatura gazu się nie zmieniła.

Oblicz ciśnienie gazu po przesunięciu tłoka.

Spośród podanych niżej zdań wybierz i podkreśl dwa poprawnie opisujące tę przemianę.

a) Energia wewnętrzna gazu wzrosła.

b) Energia wewnętrzna gazu zmalała.

c) Energia wewnętrzna gazu się nie zmieniła.

d) Gaz pobrał z otoczenia energię w postaci ciepła.

e) Gaz oddał do otoczenia energię w postaci ciepła.

f) Przemiana odbyła się bez wymiany ciepła z otoczeniem.

Zadanie 1
Wyznacz o ile zmieniła się temperatura gazu doskonałego, który zwiększył objętość z 4 dm3 do 5 dm3, jeżeli w naczyniu znajdowały się 3 mole gazu, a ciśnienie wynosiło 1050 hPa.

Zadanie 2

Korzystając z wykresu p(V) oblicz:
a) pracę wykonaną przez gaz
b) pracę wykonaną przez siły zewnętrzne
c) sprawność silnika cieplnego, który działa wg przestawionego schematu
d) nazwij kolejne przemiany, jakie zachodzą w tym silniku cieplnym

Zadanie 3
Temperatura chłodnicy silnika Carnot’a wynosi 20 0C . Temperatura grzejnika jest 3 razy większa.
A) Ile wynosi sprawność tego silnika?
B) Przedstaw na wykresie przemiany w silniku Carnot’a i nazwij je

Zadanie 4
Ile razy wzrosło ciśnienie gazu podczas przemiany izochorycznej, jeżeli jego początkowa temperatura wynosiła T1, a przyrost temperatury jest równy ∆T

Zadanie 5
W silniku Carnota temperatura grzejnika wynosi 500 K, a chłodnicy 300 K. Gaz pobiera energię w ilości 10 5 J i wykonuje pracę równą 0,2 * 10 5 J.
a) Jaką pracę (teoretycznie) może wykonać silnik, jeżeli zużyje 50 kJ ciepła?
b) Jaką pracę w rzeczywistości wykona ten silnik, jeżeli jego sprawność rzeczywista jest o 20 % mniejsza?

Zadanie 6
Ile cząsteczek zawiera gaz o objętości 20 dm3 w temperaturze 370C pod ciśnieniem 1100 hPa ?

Zadanie 7
Do wody o masie 1,5 kg o temperaturze 60 0C wlano wodę o temperaturze 25 0C. Temperatura wody po wymieszaniu wyniosła 40 0C. Ile zimnej wody wlano do ciepłej?

część 2

Stałe: R= 8,3 J/mol* K, NA = 6,02 *10 23 1/mol

Zadanie 1
Omów przemianę izobaryczną oraz:
a) przedstaw na wykresie zależności p(V), p(T), T(V)
b) jak zmienia się energia wewnętrzna gazu w tej przemianie
c) wyznacz o ile zmieniła się temperatura gazu doskonałego, który zwiększył objętość z 4 dm3 do 5 dm3, jeżeli w naczyniu znajdowały się 3 mole gazu, a ciśnienie wynosiło 1050 hPa.

Zadanie 2
a) Podaj cech gazu doskonałego.
b) Narysuj wykres p(V) cyklu przemian silnika Carnota i nazwij te przemiany.

Zadanie 3

Korzystając z wykresu p(V) oblicz:
a) pracę wykonaną przez gaz
b) pracę wykonaną przez siły zewnętrzne
c) sprawność silnika cieplnego, który działa wg przestawionego schematu
d) nazwij kolejne przemiany, jakie zachodzą w tym silniku cieplnym

Zadanie 4
Ile razy wzrosło ciśnienie gazu podczas przemiany izochorycznej, jeżeli jego początkowa temperatura wynosiła T1, a przyrost temperatury jest równy ∆T

Zadanie 5
W silniku Carnota temperatura grzejnika wynosi 500 K, a chłodnicy 300 K. Gaz pobiera energię w ilości 10 5 J i wykonuje pracę równą 0,2 * 10 5 J.
a) Jaką pracę (teoretycznie) może wykonać silnik, jeżeli zużyje 50 kJ ciepła?
b) Jaką pracę w rzeczywistości wykona ten silnik, jeżeli jego sprawność rzeczywista jest o 20 % mniejsza?

Zadanie 6
Omów przemianę izobaryczną ( i inne) oraz:
a) przedstaw na wykresie zależności p(V), p(T), V(T)
b) odpowiedz jak zmienia się energia wewnętrzna gazu poddanego zwiększaniu i zmniejszaniu objętości
c) wyznacz o ile zmieniła się temperatura gazy doskonałego, który zwiększył objętość
z 4 dm3 do 5 dm3, jeżeli w naczyniu znajdowały się 3 mole gazu.

Zadanie 7
Podaj treść II zasady termodynamiki.

Zadanie 8
Korzystając z wykresu p(V) oblicz:
a) pracę wykonaną przez gaz
b) pracę wykonaną przez siły zewnętrzne
c) sprawność silnika cieplnego, który działa wg przestawionego schematu
d) nazwij kolejne przemiany, jakie zachodzą w tym silniku cieplnym
e) przedstaw cykl przemian we współrzędnych p (T)

Zadanie 9
Do wody o masie 2 kg o temperaturze 30 0C wlano wodę o temperaturze 65 0C. Temperatura wody po wymieszaniu wyniosła 50 0C . Ile ciepłej wody wlano do zimnej?

zadanie 10
Podaj treść I zasady termodynamiki.

Rzuty i ruch po okręgu

 Zadanie 1

a) Wyraź kąt 45 stopni w radianach
b) Wyraź kąt pi/3 rad w stopniach

Zadanie 2
Wskazówka minutowa jest dwa razy krótsza od wskazówki, sekundowej, oblicz:
a) ile wynosi stosunek prędkości liniowych ich końców?
b) jak mają się do siebie przyspieszenia dośrodkowe obu wskazówek?

Zadanie 3
Z wieży o wysokości 40 m została wystrzelona poziomo z łuku strzała tak, że upadła w odległości 160 m od podstawy tej wieży. Oblicz:
a) wartość prędkości z jaką wystrzelono strzałę
b) wartość prędkości w chwili upadku strzały na ziemię
c) kąt, pod jakim wbiła się strzała w ziemię
d) wykonaj rysunek do pkt. c) - uwzględniając obliczone wielkości

Zadanie 4
Piłkę tenisową uderzono pod kątem 600 do poziomu, nadając jej taką wartość prędkości początkowej, że podczas lotu osiągnęła ona maksymalną wysokość 12 m. Oblicz:
a) wartość prędkości początkowej.
b) prędkość w najwyższym punkcie lotu piłeczki
c) wartość prędkości po upływie 0,4 s
d) czas, po jakim czasie piłeczka upadnie na ziemię
e) odległość, w jakiej od punktu uderzenia piłeczka spadnie na ziemię

Zadanie 5
Oblicz okres z jakim obracają się koła samochodu jadącego z prędkością 30 m/s, jeżeli średnica każdego z kół wynosi 40 cm.

Rzuty, ruch po okręgu

Zadanie 1. Adam o masie 80 kg siedzi na krzesełku wirującej karuzeli. Okres jego obrotu wynosi 10 sekund. Długość ramienia karuzeli wynosi 1 m. Oblicz:

a) częstotliwość ruchu karuzeli    b) prędkość w ruchu po okręgu

c) przyspieszenie  dośrodkowe

Zadanie 2. Piłkę koszykową rzucono poziomo z prędkością 10 m/s z wysokości 6 m.

a) jaką posiadała prędkość w chwili zetknięcia się z Ziemią?

b) jak  daleko upadła ta piłeczka?

Zadanie 3.  Na podstawie wykresu rzutu poziomego wyznacz: a) wysokość w rzucie  b) zasięg rzutu

Oblicz  c) prędkość początkową w tym rzucie

d) prędkość końcową w tym rzucie

e) dorysuj na wykresie obie obliczone prędkości oraz ich składowe

Zadanie 4. Piłkę tenisową uderzono pod kątem 60⁰ do poziomu, nadając jej taką wartość prędkości początkowej, że podczas lotu osiągnęła ona maksymalną wysokość 10 m. Oblicz:

a)       prędkość w najwyższym punkcie lotu piłeczki

b)       wartość prędkości początkowej.

c)       czas, po jakim czasie piłeczka upadnie na ziemię

d)       zasięg, czyli odległość, w jakiej od punktu uderzenia piłeczka spadnie na ziemię

Zadanie 5. Taternik wchodząc na szczyt upuścił czekan. Czekan spadł na ziemię po 6 sekundach, jak wysoko znadował się taternik?

 

odpowiedzi:
Zad. 4
kąt= 60 st. 1,047 rad
h= 12 m
t1= 1,55 s
vx= 8,9m/s
vy= 15,49 m/s
v= 17,8885 m/s
a) wartość prędkości początkowej.
v=18 m/s
b) prędkość w najwyższym punkcie lotu piłeczki
vx = 9 m/s
c) wartość prędkości po upływie 0,4 s
t= 0,4 s
vy= 15,5m/s
zmiana v=4 m/s
vy2= 11,5 m/s
vx= 9 m/s
v4= 14,6 m/s
d) czas, po jakim czasie piłeczka upadnie na ziemię
t= 2*t1= 3,1 s
e) odległość, w jakiej od punktu uderzenia piłeczka spadnie na ziemię
z= 27,71281292 m

Elektrostatyka ZSP

 Zadanie 1  Cztery jednakowe ładunki umieszczono w wierzchołkach kwadratu o boku a=0,2m. q=5*10-15C 

 a) wykonaj rysunek pola elektrostatycznego wokół każdego ładunku (uwzględnij oddziaływanie ładunków na siebie)

 b) oblicz potencjał elektryczny w środku kwadratu

 c) wyznacz wektor natężenie pola elektrycznego w środku kwadratu oraz jego wartość

 d) wyznacz siłę, z jaką 3 ładunki oddziaływają na 1 wybrany przez Ciebie ładunek

Zadanie 2 Dwie małe, jednakowe metalowe kulki o masach m naładowano ładunkiem elektrycznym, a następnie zawieszono u sufitu na dwu niciach o równej długości. Obie nici zaczepione są w tym samym punkcie sufitu. Pierwsza kulka posiada ładunek Q, a druga ładunek dwa razy większy. Wiszące kulki oddalone są od siebie na odległość R.

a)  wyznacz kąty zawarte między każdą z nici a sufitem.

b)  narysuj odpowiedni rysunek i przedstaw siły działające na każdą z kulek

c)  oblicz siłę oddziaływania między kulkami

d)  przedstaw schematycznie wektor natężenia pola w środku odległości pomiędzy kulkami

e)  podaj wartość natężenia pola w tym punkcie.

f)  oblicz wartość potencjału elektronu umieszczonego w 1/2 odległości między kulkami.

Zadanie 3 Płaski kondensator, w którym odległość między okładkami wynosi d=5mm, podłączono do źródła napięcia, a po naładowaniu odłączono. Obliczyć, ile razy zmieni się energia naładowanego kondensatora po całkowitym zanurzeniu go w nafcie o względnej przenikalności dielektrycznej εr =3. 

O ile należy rozsunąć okładki kondensatora aby energia ta powróciła do pierwotnej wartości? 

Zadanie 4 Dwie kulki naładowano ładunkami o wartościach Q1 = +4 C oraz Q2 = - 2C  ustawiono w odległości 0,1 m. 

a) przedstaw wektory sił na schemacie

b) oblicz siłę oddziaływania między kulkami

c) przedstaw schematycznie wektor natężenia pola w środku odległości pomiędzy kulkami

d) podaj wartość natężenia pola w tym punkcie.

e) oblicz wartość potencjału elektronu umieszczonego w ¼ odległości od ładunku dodatniego.

Zadanie 5 Wyznacz energię wewnętrzną kondensatora podłączonego do napięcia 50V, na którym znajduje się ładunek 25 mC

Zadanie 6 Kondensator płaski

a) Ile wynosi pojemność kondensatora płaskiego bez dielektryka o powierzchni okładek 0,01 m2 odległych od siebie o 0,04 m?

b) Podobny kondensator wypełniono dielektrykiem o współczynniku przenikalności elektrycznej równym 200. Jaką pojemność ma ten drugi kondensator:

c) Kondensatory (bez dielektryka i z dielektrykiem) połączono ze sobą równolegle. Ile wynosi pojemność zastępcza tego układu kondensatorów?

d) Kondensatory połączono ze sobą szeregowo. Ile wynosi pojemność zastępcza tego układu kondensatorów?

Zadanie 7 Elektron i proton umieszczone w próżni oddziaływają na siebie siłą o wartości 2,53*10-27 N. Ile wynosi odległość między tymi cząsteczkami?

Zadanie 8 Potencjał tuż przy powierzchni kropli wody o ładunku 3*10 -10 C wynosi 500 V. Oblicz promień tej kropli wody.

Zadanie 9 Korzystając z rysunku (trzy ładunki w wierzchołkach kwadratu), na którym  Q1 = + 2C, Q2 = - 1C, Q3 = + 2C, odległości a = 2 m oblicz:

a) natężenie pola w punkcie qx i qy (w czwartym wierzchołku, w środku kwadratu)

b) jaki ładunek należałoby umieścić w punkcie qx (w 4-tym wierzchołku), aby natężenie pola w środku kwadratu było równe zero ?

c) narysuj wektory natężeń w każdym wierzchołku kwadratu uwzględniając wyznaczoną wartość ładunku w punkcie b.

d) wyznacz wartości natężeń w poszczególnych wierzchołkach kwadratu.

 

Zadanie 10 Narysuj linie sił pola wokół ładunków (jeden dodatni, drugi ujemny):

a) jak oddziaływają te ładunki na siebie?

b) zaznacz linią przerywaną (lub innym kolorem) powierzchnie ekwipotencjalne w przedstawionym układzie

c) wskaż miejsca, gdzie potencjał dowolnego ładunku będzie równy zeru (przyjmij własne wartości ładunków).

Zadanie 11 Zastąp układ kondensatorów pojemnością zastępczą: (tu rysunek układu kondensatorów - podobnie jak na lekcji)

Zadanie 12 Płytki kondensatora są oddalone od siebie o 5 cm. W tej samej chwili rozpoczynają ruch od płytek dwie cząstki – elektron i proton. W którym miejscu między płytkami miną się te cząsteczki? Pomiń wzajemne oddziaływanie cząstek. Masa protonu jest 1840 razy większa od masy elektronu.. Narysuj kierunki ruchu cząsteczek między okładkami (ich położenie początkowe i końcowe.

Zadanie 14 W kondensatorze elektron porusza się między okładkami. W chwili uderzenia w okładkę ma prędkość 10  6 m/s. Odległość między okładkami wynosi 1 cm. Oblicz:

a) natężenie pola w kondensatorze

b) napięcie elektryczne między płytkami

Fale i optyka

 Fale i optyka

Zadanie 1

W kierunku stojącego chłopca nadjeżdża samochód z prędkością 90 km/h i trąbi wydając ton o częstotliwości 2000 Hz. Jaką częstotliwość dźwięku będzie słyszało to dziecko?

Zadanie 2

Oblicz częstotliwość dźwięku, jeśli odległość między sąsiednimi strzałkami fali stojącej wynosi 68 cm.

Zadanie 3

Sygnał wysłany z okrętu podwodnego powrócił do niego po 6 s. W jakiej odległości od okrętu znajduje się przeszkoda, jeśli prędkość dźwięku w wodzie wynosi 1400 m/s?

Zadanie 4

Struna gitarowa wydaje ton o częstotliwości 6300 Hz. Prędkość dźwięku w strunie wynosi 3000 m/s. Wykonaj rysunek i na jego podstawie oblicz długość tej struny.

Zadanie 5

Moc gwizdka wynosi 4π·10-8 W, próg słyszalności 10-12 W/m2. W jakiej odległości od tego gwizdka nie będzie słychać dźwięku? 

Zadanie 6

Od stojącego samochodu wydającego ton o częstotliwości 1000 Hz ucieka dziecko z prędkością 12 km/h. Jaką częstotliwość dźwięku będzie słyszało to dziecko?

Zadanie 7

Fale o zgodnych fazach docierają do punktu A w odległościach 8 i 3 m. 

Oraz teoria