Elektrostatyka

 Zadanie 1  Cztery jednakowe ładunki umieszczono w wierzchołkach kwadratu o boku a=0,2m. q=5*10-15C 

 a) wykonaj rysunek pola elektrostatycznego wokół każdego ładunku (uwzględnij oddziaływanie ładunków na siebie)

 b) oblicz potencjał elektryczny w środku kwadratu

 c) wyznacz wektor natężenie pola elektrycznego w środku kwadratu oraz jego wartość

 d) wyznacz siłę, z jaką 3 ładunki oddziaływają na 1 wybrany przez Ciebie ładunek

Zadanie 2 Dwie małe, jednakowe metalowe kulki o masach m naładowano ładunkiem elektrycznym, a następnie zawieszono u sufitu na dwu niciach o równej długości. Obie nici zaczepione są w tym samym punkcie sufitu. Pierwsza kulka posiada ładunek Q, a druga ładunek dwa razy większy. Wiszące kulki oddalone są od siebie na odległość R.

a)  wyznacz kąty zawarte między każdą z nici a sufitem.

b)  narysuj odpowiedni rysunek i przedstaw siły działające na każdą z kulek

c)  oblicz siłę oddziaływania między kulkami

d)  przedstaw schematycznie wektor natężenia pola w środku odległości pomiędzy kulkami

e)  podaj wartość natężenia pola w tym punkcie.

f)  oblicz wartość potencjału elektronu umieszczonego w 1/2 odległości między kulkami.

Zadanie 3 Płaski kondensator, w którym odległość między okładkami wynosi d=5mm, podłączono do źródła napięcia, a po naładowaniu odłączono. Obliczyć, ile razy zmieni się energia naładowanego kondensatora po całkowitym zanurzeniu go w nafcie o względnej przenikalności dielektrycznej εr =3. 

O ile należy rozsunąć okładki kondensatora aby energia ta powróciła do pierwotnej wartości? 

Zadanie 4 Dwie kulki naładowano ładunkami o wartościach Q1 = +4 C oraz Q2 = - 2C  ustawiono w odległości 0,1 m. 

a) przedstaw wektory sił na schemacie

b) oblicz siłę oddziaływania między kulkami

c) przedstaw schematycznie wektor natężenia pola w środku odległości pomiędzy kulkami

d) podaj wartość natężenia pola w tym punkcie.

e) oblicz wartość potencjału elektronu umieszczonego w ¼ odległości od ładunku dodatniego.

Zadanie 5 Wyznacz energię wewnętrzną kondensatora podłączonego do napięcia 50V, na którym znajduje się ładunek 25 mC

Zadanie 6 Kondensator płaski

a) Ile wynosi pojemność kondensatora płaskiego bez dielektryka o powierzchni okładek 0,01 m2 odległych od siebie o 0,04 m?

b) Podobny kondensator wypełniono dielektrykiem o współczynniku przenikalności elektrycznej równym 200. Jaką pojemność ma ten drugi kondensator:

c) Kondensatory (bez dielektryka i z dielektrykiem) połączono ze sobą równolegle. Ile wynosi pojemność zastępcza tego układu kondensatorów?

d) Kondensatory połączono ze sobą szeregowo. Ile wynosi pojemność zastępcza tego układu kondensatorów?

Zadanie 7 Elektron i proton umieszczone w próżni oddziaływają na siebie siłą o wartości 2,53*10-27 N. Ile wynosi odległość między tymi cząsteczkami?

Zadanie 8 Potencjał tuż przy powierzchni kropli wody o ładunku 3*10 -10 C wynosi 500 V. Oblicz promień tej kropli wody.

Zadanie 9 Korzystając z rysunku (trzy ładunki w wierzchołkach kwadratu), na którym  Q1 = + 2C, Q2 = - 1C, Q3 = + 2C, odległości a = 2 m oblicz:

a) natężenie pola w punkcie qx i qy (w czwartym wierzchołku, w środku kwadratu)

b) jaki ładunek należałoby umieścić w punkcie qx (w 4-tym wierzchołku), aby natężenie pola w środku kwadratu było równe zero ?

c) narysuj wektory natężeń w każdym wierzchołku kwadratu uwzględniając wyznaczoną wartość ładunku w punkcie b.

d) wyznacz wartości natężeń w poszczególnych wierzchołkach kwadratu.

 

Zadanie 10 Narysuj linie sił pola wokół ładunków (jeden dodatni, drugi ujemny):

a) jak oddziaływają te ładunki na siebie?

b) zaznacz linią przerywaną (lub innym kolorem) powierzchnie ekwipotencjalne w przedstawionym układzie

c) wskaż miejsca, gdzie potencjał dowolnego ładunku będzie równy zeru (przyjmij własne wartości ładunków).

Zadanie 11 Zastąp układ kondensatorów pojemnością zastępczą: (tu rysunek układu kondensatorów - podobnie jak na lekcji)

Zadanie 12 Płytki kondensatora są oddalone od siebie o 5 cm. W tej samej chwili rozpoczynają ruch od płytek dwie cząstki – elektron i proton. W którym miejscu między płytkami miną się te cząsteczki? Pomiń wzajemne oddziaływanie cząstek. Masa protonu jest 1840 razy większa od masy elektronu.. Narysuj kierunki ruchu cząsteczek między okładkami (ich położenie początkowe i końcowe.

Zadanie 14 W kondensatorze elektron porusza się między okładkami. W chwili uderzenia w okładkę ma prędkość 10  6 m/s. Odległość między okładkami wynosi 1 cm. Oblicz:

a) natężenie pola w kondensatorze

b) napięcie elektryczne między płytkami

Zadanie 15
Dwie kulki naładowano ładunkami o wartościach Q1 = +1C  oraz Q2 = - 3C i ustawiono w odległości 1 m.
a) przedstaw wektory sił na schemacie
b) oblicz siłę oddziaływania między kulkami
c) ile wyniesie wartość siły, jeżeli ładunek kulki dodatniej zwiększymy 3x ,a odległość zmniejszymy 2x?
d) przedstaw schematycznie wektor natężenia pola w środku odległości pomiędzy kulkami
e) podaj wartość natężenia pola w tym punkcie.
f) oblicz wartość potencjału elektronu umieszczonego w ¼ odległości od ładunku dodatniego.
Zadanie 16

Korzystając z rysunku, na którym  Q1 = + 2C, Q2 = - 1C, Q3 = + 2C, odległości a = 2 m oblicz:
a) natężenie pola w punkcie qx i qy
b) jaki ładunek należałoby umieścić w punkcie qx, aby natężenie pola w środku kwadratu było równe zero ?
c) narysuj wektory natężeń w każdym wierzchołku kwadratu uwzględniając wyznaczoną wartość ładunku w punkcie b.
d) wyznacz wartości natężeń w poszczególnych wierzchołkach kwadratu.
Zadanie 17
Płaski kondensator, w którym odległość między okładkami wynosi d=10 mm, podłączono do źródła napięcia, a po naładowaniu odłączono. Powierzchnia okładki kondensatora wynosi S=10 cm2. Obliczyć, ile razy zmieni się energia naładowanego kondensatora po całkowitym zanurzeniu go w nafcie o względnej przenikalności dielektrycznej εr =4. O ile należy rozsunąć okładki kondensatora aby energia ta powróciła do pierwotnej wartości? Wykonaj rysunek kondensatora.

Zadanie 18
Narysuj linie sił pola wokół ładunków:
a) jak oddziaływają te ładunki na siebie?
b) wskaż miejsca, gdzie potencjał dowolnego ładunku będzie równy zeru ( przyjmij własne wartości ładunków).

Zadanie 19
Zastąp układ kondensatorów pojemnością zastępczą:

Zadanie 20
Elektron i proton umieszczone w próżni oddziaływają na siebie siłą o wartości 2,53*10 -27. Ile wynosi odległość między tymi cząsteczkami?

Zadanie 21
Potencjał tuż przy powierzchni kropli wody o ładunku 3*10 -10C wynosi 500 V. Oblicz promień tej kropli wody.

Zadanie 22
a) Ile wynosi pojemność kondensatora płaskiego o powierzchni okładek 0,1 m2 odległych od siebie o 0,02 m?
b) Podobny kondensator wypełniono dielektrykiem o współczynniku przenikalności elektrycznej równym 200. Jaką pojemność ma ten drugi kondensator:
c) Kondensatory połączono ze sobą równolegle. Ile wynosi pojemność zastępcza tego układu kondensatorów?
d) Kondensatory połączono ze sobą szeregowo. Ile wynosi pojemność zastępcza tego układu kondensatorów?
e) Kondensator powietrzny naładowano do różnicy potencjałów 100 V. Jaki ładunek zgromadziły okładki tego kondensatora?
f) Jaką energię posiada kondensator z dielektrykiem, jeśli na jego okładkach znajduje się ładunek 3 mC?

Zadanie 23
Płytki kondensatora są oddalone od siebie o 5 cm. W tej samej chwili rozpoczynają ruch od płytek dwie cząstki – elektron i proton. W którym miejscu między płytkami miną się te cząsteczki? Pomiń wzajemne oddziaływanie cząstek.. Masa protonu jest 1840 razy większa od masy elektronu.. Narysuj kierunki ruchu cząsteczek między okładkami (ich położenie początkowe i końcowe.

Zadanie 24
W kondensatorze elektron porusza się między okładkami. W chwili uderzenia w okładkę ma prędkość 10  6 m/s. Odległość między okładkami wynosi 1 cm. Oblicz:
a) natężenie pola w kondensatorze
b) napięcie elektryczne między płytkami

 Zadanie 1

Od stojącego samochodu wydającego ton o częstotliwości 1000 Hz ucieka dziecko z prędkością 12 km/h. Jaką częstotliwość dźwięku będzie słyszało to dziecko?

Zadanie 2

W kierunku stojącego chłopca nadjeżdża samochód z prędkością 90 km/h i trąbi wydając ton o częstotliwości 2000 Hz. Jaką częstotliwość dźwięku będzie słyszało to dziecko?

Zadanie 3

Fale o zgodnych fazach spotykają się w punkcie P i pokonują drogi 20 m i 15 m. Jaka fala będzie w punkcie spotkania 

a) o długoości 2 m 

b) o długości 3m

Zadanie 4

Oblicz częstotliwość i okres dźwięku, jeśli długość fali  wynosi  68 cm. narysuj falę  o amplitudzie 20 cm

Zadanie 5

Moc gwizdka wynosi 4π·10^-8 W, próg słyszalności 10^-12 W/m². W jakiej odległości od tego gwizdka nie będzie słychać dźwięku? 

Oraz teoria

BRYŁA

zad.1 . a) Oblicz stosunek energii kinetycznej ruchu obrotowego do postępowego dla kuli toczącej się bez poślizgu po równi pochyłej.
b) jakie będzie przyspieszenie kuli przy staczaniu się z równi o kącie nachylenia 45 stopni

zad.2 Oblicz moment bezwładności układu kul o promieniach R i masach m według rysunku:

zad.3 Oblicz siły nacisku belki na punkty podparcia, jeżeli masa belki wynosi 100 kg, jej długość 4 m, co przedstawia rysunek:

zad.4. Koło zamachowe o momencie bezwładności I = 0,2 kgm2 obraca się wokół poziomej osi przechodzącej przez jego środek, wykonując n = 600 obr/min. Przy hamowaniu koło zatrzymuje się po upływie czasu Δt = 20 s. Znajdź moment siły hamującej i liczbę obrotów do chwili zatrzymania.
odp: M = 0,2π Nm, N=100 obr.
zad.5. Na rurę o cienkich ściankach nawinięto nić, której wolny koniec przymocowano do sufitu. Rura odkręca się z nici pod działaniem własnego ciężaru (rys.). Znajdź przyspieszenie rury i siłę napięcia nici, jeżeli masę i grubość nici można zaniedbać. Początkowa długość nici jest dużo większa od promienia rury. Ciężar rury wynosi Q.

zad.6. Przez bloczek zawieszony na poziomej osi przerzucono nieważką i nierozciągliwą nić, do końców której przymocowano ciężarki o masach m1 = 0,5 kg i m2 = 0,2 kg. Masa bloczka wynosi m = 0,4 kg. Bloczek traktujemy jako jednorodny krążek. Znajdź liniowe przyspieszenie ciężarków. Przyjmij, że nić nie ślizga się po bloczku.
zad.7 Z równi pochyłej o kącie nachylenia α stacza się bez poślizgu ciało o momencie bezwładności I, masie m i promieniu r. Wyznacz jego przyspieszenie liniowe, kątowe i siłę tarcia.
zad.8. Pełne, jednorodne ciała: walec i kula staczają się bez poślizgu z równi pochyłej o kącie nachylenia α i wysokości h. Masy i promienie tych ciał są jednakowe. Które z nich stoczy się wcześniej?
zad.9. Kula o początkowej prędkości w ruchu postępowym v0 = 10 m/s wtacza się bez poślizgu na równię pochyłą o kącie nachylenia 45 st. Jaką drogę przebędzie kula po równi do chwili zatrzymania się i po jakim czasie wróci do podstawy równi?

zad.10. Środek masy kuli bilardowej posiada początkową prędkość v0. Promień kuli wynosi R, jej masa M, a współczynnik tarcia pomiędzy kulą i stołem jest równy µ. Jak daleko przesunie się kula po stole, zanim przestanie się ślizgać?

zad.11. W czasie pokazów gimnastyki artystycznej można oglądać ćwiczenie, w którym obręcz rzucona przez zawodniczkę tocząc się początkowo z poślizgiem wraca ku niej i w końcowej fazie ruchu toczy się już bez poślizgu. Jest to możliwe, jeżeli w czasie rzutu zawodniczka nada obręczy ruch obrotowy o odpowiednim kierunku. Znajdź związek pomiędzy początkową wartością prędkości ruchu postępowego v0 i prędkości kątowej ω0.
zad.12. Po idealnie gładkiej poziomej powierzchni ślizga się bez obrotów walec. Prędkość liniowa środka masy wynosi v0, a kierunek prędkości jest prostopadły do osi walca. W pewnej chwili powierzchnia pod walcem staje się szorstka, a współczynnik tarcia posuwistego przyjmuje wartość f. Po jakim czasie walec będzie się toczył bez poślizgu i jaka będzie wtedy prędkość jego środka masy?
zad.13. Kołowrót o masie m, momencie bezwładności I0 i promieniach zewnętrznym R oraz wewnętrznym r leży na płaszczyźnie poziomej (rys.). Na kołowrót nawinięta jest nić, do której przyłożono siłę F. Opisz ruch kołowrotu w zależności od kąta α jaki tworzy nić z kierunkiem poziomym.

niedziela, 15 grudnia 2024

OPTYKA

Zadanie 1
Soczewka szklana dwuwypukła ma promienie krzywizn równe: R1= R2 = 8 cm, n_szk=2,4.
a) ile wynosi ogniskowa tej soczewki.
b) Jaka jest odległość przedmiotu od soczewki, jeżeli obraz znajduje się w odległości 6 cm od soczewki
c) Ile wynosi powiększenie soczewki?
d) Wykonaj rysunek soczewki
e) ile wynosi zdolność skupiająca tej soczewki

Zadanie 2
Dzięki okularom o zdolności skupiającej Zok = -4 D krótkowidz widzi dobrze przedmioty z odległości dobrego widzenia oka normalnego (d= 25 cm). Z jakiej odległości widzi on dobrze bez okularów?

Zadanie 3 Bezwzględny współczynnik załamania szkła jest równy n = 1,5. Światło pada prostopadle na szybę o grubości 0,2 cm. Ile wynosi czas przejścia światła przez szybę?

Zadanie 4
Wklęsłe zwierciadło kuliste ma ogniskową f= 6 cm. Odległość przedmiotu od zwierciadła wynosi 4cm.
a) Oblicz odległość obrazu od zwierciadła.
b) Podaj cechy obrazu
c) Wykonaj rysunek zwierciadła.
d) ile wynosi promień krzywizny tego zwierciadła ?

Zadanie 5
Ile prążków i o jakiej barwie można otrzymać na ekranie o szerokości 80 cm ustawionym w odległości 2m od siatki dyfrakcyjnej, na której nacięto 200 rys na 1 mm, jeśli na te siatkę pada światło zielone o długości 530 nm. Do obliczeń możesz przyjąć, że kąt ugięcia światła jest mały, i że sin α ≈ tg α

Ponadto:
Wykonaj rysunek oka i opisz wszystkie znane Ci elementy jego budowy.

Krótkowzroczność i dalekowzroczność

Obraz w mikroskopie, lupie i lunecie.

Odbicie i załamanie

Interferencja

Przejście światła przez pryzmat.

Kąt graniczny

Kąt Brewstera

Polaryzacja

Zadanie 1
Promień światła monochromatycznego pada na powierzchnię wody pod kątem 45°. Oblicz:
- kąt załamania promienia w wodzie, nw= 4/3 (2 pkt)
- kąt między promieniem odbitym a załamanym, (2 pkt)
- szybkość światła w wodzie (2 pkt)
- wykonaj rysunek do tego zadania (2 pkt)

Zadanie 2
Dzięki okularom o zdolności skupiającej Zok = -4 D krótkowidz widzi dobrze przedmioty z odległości dobrego widzenia oka normalnego (d= 25 cm). Z jakiej odległości widzi on dobrze bez okularów? (3 pkt)

Zadanie 3 Bezwzględny współczynnik załamania szkła jest równy n = 1,5. Światło pada prostopadle na szybę o grubości 0,2 cm. Ile wynosi czas przejścia światła przez szybę?

Zadanie 4
Wklęsłe zwierciadło kuliste ma ogniskową f= 6 cm. Odległość przedmiotu od zwierciadła wynosi 4cm.
a) Oblicz odległość obrazu od zwierciadła. (2 pkt)
b) Podaj cechy obrazu(2 pkt)
c) Wykonaj rysunek zwierciadła. (2 pkt)
d) ile wynosi promień krzywizny tego zwierciadła ? (2 pkt)

Zadanie 5
Soczewka szklana dwuwypukła ma promienie krzywizn równe: R1= R2 = 8 cm, n_szk=2,4.
a) ile wynosi ogniskowa tej soczewki. (2 pkt)
b) Jaka jest odległość przedmiotu od soczewki, jeżeli obraz znajduje się w odległości 6 cm od soczewki (2 pkt)
c) Ile wynosi powiększenie soczewki? (2 pkt)
d) Wykonaj rysunek soczewki (2 pkt)
e) ile wynosi zdolność skupiająca tej soczewki (2 pkt)



i jeszcze:
Zadanie 1 Oblicz zdolność skupiającą soczewki o ogniskowej f = 50 cm

Zadanie 2
Wklęsłe zwierciadło kuliste ma ogniskową równą 4 cm.
a) W jakiej odległości od zwierciadła kulistego należy umieścić przedmiot, aby obraz był odległy o 6 cm od zwierciadła? (2 pkt)
b) wykonaj rysunek dla tego zwierciadła (2 pkt)
c) podaj cechy obrazu (2 pkt)
d) ile wynosi promień krzywizny tego zwierciadła ? (2 pkt)

Zadanie 3
Soczewka szklana dwuwypukła ma promienie krzywizn równe: R1= R2 = 10 cm, n_szk=2..
a) ile wynosi ogniskowa tej soczewki? (2 pkt)
b) Jaka jest odległość przedmiotu od soczewki, jeżeli obraz znajduje się w odległości 6 cm od soczewki (2 pkt)
c) Ile wynosi powiększenie soczewki? (2 pkt)
d) Wykonaj rysunek soczewki (2 pkt)
e) ile wynosi zdolność skupiająca tej soczewki (2 pkt)

wtorek, 19 listopada 2024

HYDROSTATYKA

 TEORIA

1. Podaj cechy gazu doskonałego. Równanie gazu doskonałego. Zasady termodynamiki
2. Omów przemianę izotermiczną, izobaryczną, izochoryczną, adiabatyczną
- przedstaw na wykresie zależności p(V), p(T), V(T) w tej przemianie
- podaj zależności fizyczne między parametrami gazu w tej przemianie (równanie gazu doskonałego)
3. Narysuj cykl przemian silnika Carnota i nazwij je

ZADANIA:
zad. 1 W butli o pojemności 50l znajduje się tlen. Temp. początkowa wynosi 280 K, a ciśnienie 100 kPa. Butla na słońcu nagrzała się do temp. 430 K, a ciśnienie  wyniosło 120 kPa.   Oblicz liczbę moli, Tk oraz ciepło dostarczone przez słońce.

zad 2.

W naczyniu znajdował się gaz pod ciśnieniem 2·105 Pa i o temperaturze 25 °C, zamknięty tłokiem o powierzchni przekroju 50 cm2. Początkowo objętość gazu wynosiła 1000 cm3, a następnie przesunięto tłok o 5 cm w prawo, jak pokazano na rysunku. Temperatura gazu się nie zmieniła.

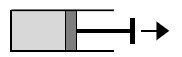
Oblicz ciśnienie gazu po przesunięciu tłoka.

Spośród podanych niżej zdań wybierz i podkreśl dwa poprawnie opisujące tę przemianę.

a) Energia wewnętrzna gazu wzrosła.

b) Energia wewnętrzna gazu zmalała.

c) Energia wewnętrzna gazu się nie zmieniła.

d) Gaz pobrał z otoczenia energię w postaci ciepła.

e) Gaz oddał do otoczenia energię w postaci ciepła.

f) Przemiana odbyła się bez wymiany ciepła z otoczeniem.

Zadanie 1
Wyznacz o ile zmieniła się temperatura gazu doskonałego, który zwiększył objętość z 4 dm3 do 5 dm3, jeżeli w naczyniu znajdowały się 3 mole gazu, a ciśnienie wynosiło 1050 hPa.

Zadanie 2

Korzystając z wykresu p(V) oblicz:
a) pracę wykonaną przez gaz
b) pracę wykonaną przez siły zewnętrzne
c) sprawność silnika cieplnego, który działa wg przestawionego schematu
d) nazwij kolejne przemiany, jakie zachodzą w tym silniku cieplnym

Zadanie 3
Temperatura chłodnicy silnika Carnot’a wynosi 20 0C . Temperatura grzejnika jest 3 razy większa.
A) Ile wynosi sprawność tego silnika?
B) Przedstaw na wykresie przemiany w silniku Carnot’a i nazwij je

Zadanie 4
Ile razy wzrosło ciśnienie gazu podczas przemiany izochorycznej, jeżeli jego początkowa temperatura wynosiła T1, a przyrost temperatury jest równy ∆T

Zadanie 5
W silniku Carnota temperatura grzejnika wynosi 500 K, a chłodnicy 300 K. Gaz pobiera energię w ilości 10 5 J i wykonuje pracę równą 0,2 * 10 5 J.
a) Jaką pracę (teoretycznie) może wykonać silnik, jeżeli zużyje 50 kJ ciepła?
b) Jaką pracę w rzeczywistości wykona ten silnik, jeżeli jego sprawność rzeczywista jest o 20 % mniejsza?

Zadanie 6
Ile cząsteczek zawiera gaz o objętości 20 dm3 w temperaturze 370C pod ciśnieniem 1100 hPa ?

Zadanie 7
Do wody o masie 1,5 kg o temperaturze 60 0C wlano wodę o temperaturze 25 0C. Temperatura wody po wymieszaniu wyniosła 40 0C. Ile zimnej wody wlano do ciepłej?

część 2

Stałe: R= 8,3 J/mol* K, NA = 6,02 *10 23 1/mol

Zadanie 1
Omów przemianę izobaryczną oraz:
a) przedstaw na wykresie zależności p(V), p(T), T(V)
b) jak zmienia się energia wewnętrzna gazu w tej przemianie
c) wyznacz o ile zmieniła się temperatura gazu doskonałego, który zwiększył objętość z 4 dm3 do 5 dm3, jeżeli w naczyniu znajdowały się 3 mole gazu, a ciśnienie wynosiło 1050 hPa.

Zadanie 2
a) Podaj cech gazu doskonałego.
b) Narysuj wykres p(V) cyklu przemian silnika Carnota i nazwij te przemiany.

Zadanie 3

Korzystając z wykresu p(V) oblicz:
a) pracę wykonaną przez gaz
b) pracę wykonaną przez siły zewnętrzne
c) sprawność silnika cieplnego, który działa wg przestawionego schematu
d) nazwij kolejne przemiany, jakie zachodzą w tym silniku cieplnym

Zadanie 4
Ile razy wzrosło ciśnienie gazu podczas przemiany izochorycznej, jeżeli jego początkowa temperatura wynosiła T1, a przyrost temperatury jest równy ∆T

Zadanie 5
W silniku Carnota temperatura grzejnika wynosi 500 K, a chłodnicy 300 K. Gaz pobiera energię w ilości 10 5 J i wykonuje pracę równą 0,2 * 10 5 J.
a) Jaką pracę (teoretycznie) może wykonać silnik, jeżeli zużyje 50 kJ ciepła?
b) Jaką pracę w rzeczywistości wykona ten silnik, jeżeli jego sprawność rzeczywista jest o 20 % mniejsza?

Zadanie 6
Omów przemianę izobaryczną ( i inne) oraz:
a) przedstaw na wykresie zależności p(V), p(T), V(T)
b) odpowiedz jak zmienia się energia wewnętrzna gazu poddanego zwiększaniu i zmniejszaniu objętości
c) wyznacz o ile zmieniła się temperatura gazy doskonałego, który zwiększył objętość
z 4 dm3 do 5 dm3, jeżeli w naczyniu znajdowały się 3 mole gazu.

Zadanie 7
Podaj treść II zasady termodynamiki.

Zadanie 8
Korzystając z wykresu p(V) oblicz:
a) pracę wykonaną przez gaz
b) pracę wykonaną przez siły zewnętrzne
c) sprawność silnika cieplnego, który działa wg przestawionego schematu
d) nazwij kolejne przemiany, jakie zachodzą w tym silniku cieplnym
e) przedstaw cykl przemian we współrzędnych p (T)

Zadanie 9
Do wody o masie 2 kg o temperaturze 30 0C wlano wodę o temperaturze 65 0C. Temperatura wody po wymieszaniu wyniosła 50 0C . Ile ciepłej wody wlano do zimnej?

zadanie 10
Podaj treść I zasady termodynamiki.

wtorek, 8 października 2024

HYDROSTATYKA

HYDROSTATYKA
1. Klocek drewniany o masie 0,4 kg zawieszony na siłomierzu zanurzono do połowy w wodzie. Jaką wartość siły wskazuje siłomierz? Gęstość wody 1000 kg/m3, a drewna 600 kg/m3.
2. Oblicz gęstość drewna, z którego wykonano klocek sześcienny, jeżeli po wrzuceniu go do nafty o gęstości 0,8 g/m3, pływa zanurzony do 4/5 swej wysokości.
3. Bryłkę metalu o objętości 100 cm3 zawieszono w powietrzu na siłomierzu, który wskazał 8 N. Jaka wartość wskaże siłomierz, gdy bryłkę zanurzymy w wodzie o gęstości 1000 kg/m3?
4. Jaka musi być co najmniej powierzchnia kry lodowej grubości 25 cm, aby uniosła człowieka o masie 70 kg? Gęstość lodu wynosi 920 kg/m3, a wody 1000 kg/m3.
5. Ile wynosi objętość góry lodowej pływającej w morzu, jeżeli wystająca część ma objętość 10000 m3? Gęstość lodu wynosi 920 kg/m3, a wody 1000 kg/m3.
6. Oblicz gęstość jednorodnego ciała, którego ciężar w powietrzu Qp = 2,8 N, a wodzie Qw = 1,8 N. Siłę wyporu powietrza pomijamy. Gęstość wody ρw = 1000 kg/m3.
7. Ciężar pewnego ciała zanurzonego w odzie jest n = 3 razy mniejszy od ciężaru tego ciała w powietrzu. Ile wynosi gęstość tego ciała?
8. Kawałek jednorodnego metalu zanurzony w wodzie waży Q1 = 0,79 N, a zanurzony w nafcie waży Q2 = 0,81 N. a) Jaka jest gęstość tego metalu? b) Jaką objętość ma kawałek metalu?
9. Kawałek stopu miedzi i cynku w powietrzu waży P = 0,16 N, a w wodzie Q = 0,14 N. Oblicz skład procentowy tego stopu (wagowo). Gęstość miedzi ρCu = 8960 kg/m3, zaś cynku ρZn = 7100 kg/m3.
10. Jednorodny sześcian pływa w rtęci, przy czym 1/5 części jego objętości jest zanurzona. Jeśli na nim postawimy drugi sześcian o takich samych wymiarach, to sześcian dolny zanurzy się do połowy swojej objętości. Znajdź gęstość drugiego sześcianu. Gęstość rtęci wynosi 13,6*103 kg/m3.
11. Probówka ze śrutem o masie 0,02 kg zanurza się w cieczy o gęstości 800 kg/m3 do pewnej głębokości. Po wrzuceniu do probówki ciężarka o masie 0,05kg zanurza się ona do tej samej głębokości w innej cieczy. Oblicz gęstość tej cieczy.
12. Na powierzchni morza dryfuje bryła lodu. Część tej bryły o V= 300m3 wystaje ponad poziom wody. Oblicz
a) V całej bryły
B) V zanurzonej części bryły d wody = 1030kg/m3 d lodu= 900kg/m3
13. Jeden koniec rurki w kształcie litery U jest zamknięty, a drugi otwarty. W rurce znajduje się rtęć, przy czym w zamkniętym ramieniu jest jej więcej o 1 cm. Jakie ciśnienie panuje w zamkniętej części rurki, jeśli ciśnienie atmosferyczne wynosi 770mmHg.
14. Do rurki w kształcie litery U wlano rtęć, a następnie dolano wody. Zmierzono, ze różnica poziomu cieczy w obu tych naczyniach wynosi 25cm. Oblicz h słupa wody. (drtęci = 13 600 kg/m3)
15. Jednorodny sześcian pływa w rtęci przy czym 1/5 części jego objętości jest zanurzona. Jeśli na nim postawimy drugi sześcian o takich samych wymiarach, to sześcian dolny zanurzy się do polowy swojej objętości. Znajdź gęstość drugiego sześcianu. Gęstość rtęci wynosi 13,6 * 10³ kg/m²
16. Do słoika nalano 5cm rtęci (gęstość rtęci=3600 kg/m3) a następnie 15cm wody(gęstość wody=1000 kg/m3). Jakie ciśnienie wywierają te mieszaniny na dno naczynia?
17. Do naczynia w kształcie litery U nalano wody a następnie z jednej strony dolano nafty (gęstość nafty=8000 kg/m3). Jaka była różnica wysokości słupków nafty i wody?
18. W wodzie pływa drewniana kula o objętości 120cm3. Jaka jest gęstość drewna jeżeli wiadomo że 40cm3 objętości kuli wystaje nad powierzchnię wody.
19. W wodzie pływa drewniany klocek o gęstości 400 kg/m3 tak że 72cm3 klocka wystaje nad powierzchnię wody. Jaka jest objętość zanurzonej części klocka?
20. Przedmiot o gęstości 900kg/m3 jest częściowo zanurzony w wodzie. Oblicz jaki jest stosunek wystającej części do zanurzonej?
21. Kuleczka zawieszona na siłomierzu waży w powietrzu 80N, a całkowicie zanurzona w wodzie waży 70N. Jaka jest wartość siły wyporu oraz objętość kuleczki?
22. Kuleczka zawieszona na siłomierzu waży w powietrzu 80N, a całkowicie zanurzona w wodzie waży 70N. Oblicz jaka jest gęstość kuleczki?
23. Kuleczka metalowa zawieszona na siłomierzu waży 45N. Jaka na tę kuleczkę działa siła wyporu po całkowitym zanurzeniu w wodzie? Jaki jest pozorny ciężar wskazywany przez siłomierz gdy widomo ze średnia gęstość wynosi 1500kg/m3?
24. Do wody pionowo w dół wpada kuleczka drewniana o gęstości 400 kg/m3 z prędkością 12m/s. Oblicz na jakiej drodze zatrzyma się ta kuleczka? Pomiń opory.
25. Z głębokości h=1,2m wypływa na powierzchnię wody kuleczka drewniana o gęstości 400 kg/m3. Oblicz na jaką wysokość kuleczka wyskoczy z wody. Pomiń opory.
26. Do naczynia w kształcie walca o promieniu podstawy 0,1m wlano ?dm3 objętości wody i 2?dm3 objętości nafty(800kg/m3). Oblicz ciśnienie hydrostatyczne na dnie naczynia.
27. Do naczynia w kształcie litery U nalano wody a następnie z jednej strony dolano nafty (gęstość nafty=8000 kg/m3. Wysokość słupa nafty wyniosła 18cm. Jaka była różnica wysokości nafty i wody?
28. W wodzie zanurzone zostało pewne ciało. Pomiar siły wyporu działającej na ciało dał wynik 10 N. Jaka jest objętość tego ciała?
29. Na powierzchni morza dryfuje Bryła lodu. Cześć tej bryły o V= 300m3 wystaje ponad poziom wody. Oblicz V całej bryły d wody = 1030kg/m3 d lodu= 900kg/m3
30. Jeden koniec rurki w kształcie litery U jest zamknięty, a drugi otwarty. W rurce znajduje się rtęć, przy czym w zamkniętym ramieniu jest jej więcej o 1cm. Jakie ciśnienie panuje w zamkniętej części rurki, jeśli ciśnienie atmosferyczne wynosi 770mmHg.
31. Oblicz ciśnienie, które wywiera klocek o masie m = 5kg na powierzchnię S = 25 cm2
32. Kula metalowa waży w powietrzu 140N a zawieszona na siłomierzu w wodzie 120N. Jaka siła wyporu działa na kuleczkę w wodzie? Jaka jest objętość kuli gdy gęstość wody wynosi 1000?
33. Z jakim przyśpieszeniem wyskoczy na powierzchnię wody kuleczka drewniana o gęstości 2 razy mniejszej niż gęstość wody. Pomiń opory.
34. Kula metalowa waży w powietrzu 140N a zawieszona na siłomierzu w wodzie 120N. Jaka jest jej masa?
35. Do rurki w kształcie litery U wlano rtęć, a następnie dolano wody. Zmierzono, że różnica poziomu cieczy w obu tych naczyniach wynosi 25cm. Oblicz h słupa wody. (d rtęci = 13 600 kg/m3)

czwartek, 5 września 2024

Ruch drgający klasa 3t

1. Klocek zaczepiony na swobodnym końcu liniowej sprężyny, zaczepionej drugim końcem do ściany porusza się w płaszczyźnie poziomej bez tarcia. Okres ruchu klocka wynosi T zaś prędkość klocka w chwili przechodzenia przez położenie równowagi wynosi v1. Oblicz amplitudę drgań klocka. Napisz równanie ruchu klocka wiedząc, że w chwili początkowej jego wychylenie z położenia równowagi było N razy mniejsze od wychylenia maksymalnego?
2. Ciało o masie 40 g zostało zawieszone na sprężynie o stałej 40 N/m. Jaki będzie okres drgań tej masy na tej sprężynie?
3. Oscylator harmoniczny o masie 3 g wykonuje drgania o amplitudzie 1 cm. Całkowita energia tego oscylatora jest równa 2 mJ. Jaki jest jego okres drgań?
4. Energia całkowita drgania harmonicznego zmalała 16 razy w pewnym okresie czasu. Ile razy zmalała amplituda drgań w czasie dwa razy dłuższym?
5. Na sprężynie o stałej sprężystości k wisi skrzynka o masie m. W pewnej chwili na skrzynce siadł kot o masie mk, wskutek czego skrzynka zaczęła poruszać się ruchem harmonicznym prostym. Oblicz okres drgań skrzynki z kotem oraz maksymalną wartość siły bezwładności działającej na kota.
6. Długość wahadła matematycznego zmalała 2 razy. Ile razy zmienił się okres drgań?
7. Drewniany klocek w kształcie sześcianu o boku 1 cm i gęstości 0.8 g/cm3 pływa w wodzie i wykonuje małe drgania pionowe. Jaki jest ich okres?
8. Naszkicować obraz widoczny na ekranie oscyloskopu, będący złożeniem dwu prostopadłych drgań harmonicznych, jednego o częstotliwości 100 Hz (wzdłuż osi X), drugiego o częstotliwości 50 Hz (wzdłuż osi Y). Faza początkowa obu drgań 0.
9. Oscylator harmoniczny wykonuje drgania o amplitudzie 1 cm i okresie 0.2 s. Jak jest maksymalna prędkość i maksymalne przyśpieszenie tego oscylatora?
10. Napisać równanie wiążące siłę i energię potencjalną.
11. Ciężarek o masie m zawieszono na sprężynie o współczynniku sprężystości k. Po wychyleniu go z położenia równowagi do dołu o 3 cm okres drgań ciężarka był równy 2 s. Jaki byłby okres drgań tego ciężarka, gdyby jego wychylenie wynosiło 1 cm?
12. Długość wahadła matematycznego zmniejszono 16 razy. Jak zmienił się okres drgań tego wahadła?
13. Oblicz:
- okres
- częstotliwość
- amplitudę
- częstość kołową
- prędkość maksymalną
- przyspieszenie maksymalne
- największą siłę, gdy m=2kg
dla wychylenia określonego równaniem:
x = 2,5 sin (π/3 * t) .
Przedstaw na wykresie x (t), v(t), a(t)
14. Amplituda drgań harmonicznych wynosi 12 cm, zaś częstotliwość 0,5 Hz. Zapisz równanie tego ruchu.
15. Wyznacz długość wahadła matematycznego o okresie drgań 0,2 s.
16.W ciągu jakiego czasu od początku ruchu punkt drgający harmonicznie wychyli się z położenia równowagi o połowę amplitudy? Okres drgań jest równy 24 s, a faza początkowa równa się zeru
17. Znaleźć fazę początkową drgań ciała, jeżeli po czasie t = 0,25 s od chwili początkowej wychylenie było równe połowie amplitudy. Okres drgań T = 6 s.
18. Faza początkowa drgań harmonicznych jest równa zeru. W ciągu jakiej części okresu prędkość punktu stanie się równa połowie jego prędkości maksymalnej.
19. Po jakim czasie od rozpoczęcia ruchu punkt drgający według równania x = 7 sin 0,5t przebywa drogę od położenia równowagi do największego wychylenia?
20. Amplituda drgań harmonicznych jest równa 5 cm, zaś okres 4 s. Znaleźć maksymalną prędkość drgającego punktu i jego maksymalne przyśpieszenie.
21. Równanie ruchu punktu dane jest w postaci x = 2 sin(Pt/2 ) cm. Znaleźć:
1) okres drgań,
2) maksymalną prędkość punktu,
3) jego maksymalne przyśpieszenie.
22. Napisać równanie ruchu drgającego harmonicznego, jeśli maksymalne przyśpieszenie punktu wynosi 49,3 cm/s2, okres drgań 2 s, a początkowe wychylenie punktu z położenia równowagi 25 mm.
23. Amplituda drgań harmonicznych punktu materialnego A = 2 cm, zaś energia całkowita drgań E = 3•10-7 J. Przy jakim wychyleniu z położenia równowagi na drgający punkt działa siła F = 2,25•10-5 N?
23. Areometr o masie m =0,2kg pływa w cieczy. Gdy zanurzy się go nieco w cieczy i puści, to zacznie on wykonywać drgania z okresem T=3,4s. Przyjmując, że drgania nie są tłumione, znaleźć gęstość cieczy , w której pływa areometr. Średnica pionowej walcowatej rurki areometru jest równa d=1cm.
24. Do naczynia w kształcie litery U i przekroju poprzecznym S wlano masę m wody o gęstości g . Słup cieczy wprawiono w drgania. Obliczyć okres tych drgań.
25. Ciało o masie 5 g wykonuje drganie, które w układzie SI opisać można równaniem liczbowym x = 0,1 sin 0,5 P t . Znaleźć liczbowe wartości energii kinetycznej i potencjalnej ciała po upływie 20 s od chwili początkowej. Jaka jest całkowita energia ciała?
26. Jaki jest stosunek energii kinetycznej punktu drgającego harmonicznie do jego energii potencjalnej w chwilach, gdy wychylenie punktu z położenia równowagi wynosi: a) x = A/4, b) x = A/2 c) x = A, gdzie A - amplituda drgań.

Pole magnetyczne kl. Vt

zad. 1. Oblicz natężenie prądu płynącego w prostoliniowym przewodniku jeżeli w odległości 0,1 cm od przewodnika wartość wektora indukcji magnetycznej B = 4*10-6 T.
Jaka jest wartość napięcia przyłożonego do końców przewodnika jeżeli jego opór jest równy 20 Ω ?

zad. 2. Przez zwojnicę posiadającą 100 zwojów i mającą długość 20 cm płynie prąd. Zwojnica jest połączona ze źródłem o SEM 4,5 V.
a) Oblicz wartość natężenia tego prądu, jeżeli wewnątrz zwojnicy zostało wytworzone pole magnetyczne o indukcji, której wartość wynosi 0,0025 T.
b) narysuj zwojnicę oraz linie pola magnetycznego wytworzonego przez nią, zaznacz ich zwrot we wnętrzu i na zewnątrz zwojnicy. Zaznacz bieguny źródła prądu.
c) Jak zmieni się indukcja pola wewnątrz zwojnicy, jeśli do jej wnętrza zostanie wsunięty rdzeń o współczynniku przenikalności 100.
d) oblicz opór zwojnicy.
e)do przedstawionego obwodu dołączono opornicę suwakową, w taki sposób, aby można było zmieniać natężenie prądu płynącego w obwodzie. Narysuj schemat tego obwodu.

zad. 3. Pręt o masie 100g i długości 1m wisi poziomo w prostopadłym do niego polu magnetycznym o indukcji 0,2T. Oblicz natężenie prądu, który musiałby płynąć przez pręt, aby siła elektrodynamiczna zrównoważyła siłę ciężkości.

zad. 4. Oblicz jaka powinna być masa ciała o ładunku e = - 2 *10 -6 C, poruszającego się z prędkością v = 0,6 km/minutę, by w polu magnetycznym o indukcji B = 18*10-4 T torem ruchu tego ciała był okrąg o średnicy 100 m.
Wykonaj rysunek ruchu ciała w polu magnetycznym.

zad.5
a) Dorysuj jedną z trzech wielkości: indukcję , siłę lub natężenie prądu na załączonych rysunkach:


b) Ustal znak ładunku, zaznacz jedną z wielkości: indukcję, prędkość lub siłę



Zad. 6. W dwóch długich, równoległych i ustawionych do płaszczyzny rysunku przewodnikach płyną prądy w tych samych kierunkach. W jakiej odległości od pierwszego przewodnika indukcja magnetyczna jest równa zero?


Zad. 7. Cząstka α wpada w pole magnetyczne o indukcji B=0.02T prostopadle do kierunku wektora indukcji B i zatacza krąg o promieniu r=0.2m. Oblicz energię cząstki (w J i keV).

Zad. 8. Oblicz natężenie pola magnetycznego w środku kwadratu (lub prostokąta) o boku a (lub bokach a,b), utworzonego przez cztery nieskończenie długie przewodniki z prądem.

Zad.9. Proton poruszający się z prędkością 10 do potęgi 5 m/s wpada w jednorodne pole magnetyczne o indukcji B = 2T pod kątem 45 stopni do kierunku wektora B. Ile wynosi promień i skok śruby po której porusza się proton.

Zad.10. Jaką szybkość ma proton, jeżeli bez odchylenia od swojego pierwotnego przechodzi przez układ prostopadłych do siebie pól: magnetycznego o indukcji B=2T i elektrycznego o natężeniu E=1000 V/m. Prędkość protony jest prostopadła zarówno do E jak i B.

Teoria
1. Budowa i działanie cyklotronu.
2. Siła elektrodynamiczna i siła Lorentza
3. Rysunki pola magnetycznego (magnes, zwojnica, przewodnik z prądem)
4. Zjawisko magnesowania (ferro-, para- i diamagnetyki)
5. Oddziaływanie przewodników z prądem na siebie

poniedziałek, 22 kwietnia 2024

Grawitacja

GRAWITACJA
Zadanie 1. Zakładasz, że satelita znajduje się na orbicie stacjonarnej, gdy porusza się po okręgu współśrodkowym z równikiem oraz znajduje się cały czas nad tym samym miejscem na powierzchni Ziemi. Dana jest masa Ziemi Mz oraz stała grawitacji G.
a)Wyznacz promień orbity stacjonarnej satelity Ziemi
b)Oblicz prędkość satelity na tej orbicie.
Zadanie 2. Trzy jednakowe małe jednorodne kulki, każda o masie m, rozmieszczono tak, jak na rysunku. Bok kwadratu ma długość ½ m.
a)Wyznacz wartość natężenia pola grawitacyjnego wytworzonego przez układ kulek w punkcie A:
b)Uzupełnij rysunek – narysuj wektor natężenia pola grawitacyjnego w punkcie A
Zadanie 3. Na powierzchni Księżyca przyspieszenie grawitacyjne wynosi 0,16 przyspieszenia ziemskiego. Promień Księżyca wynosi 1470 km.
a) Wyznacz pierwszą prędkość kosmiczną dla Księżyca
b) Jaką prędkość musiałaby mieć rakieta na Księżycu, aby móc powrócić na Ziemię?
c) Ile waży na Księżycu osoba o masie 50 kg?
Zadanie 4. Podaj treść I, II, III prawa Keplera. Wyjaśnij pojęcia związane z tymi prawami.
Zadanie 5. Jowisz ma masę 315 razy większą niż Ziemia, a jego promień jest 11 razy większy od promienia Ziemi.
a) wyznacz przyspieszenie grawitacyjne na Jowiszu
b) Wyznacz pierwszą prędkość kosmiczną dla tej planety
c) Jaką prędkość musiałaby mieć rakieta na Jowiszu, aby móc powrócić na Ziemię ?
Zadanie 6. Dwoje studentów siedzi w bibliotece w odległości 1m od siebie, masa studentki wynosi 60kg, a studenta 70kg. Jaką siłą oddziaływają na siebie.
Wykonaj rysunek sił.
Zadanie 7. Mars jest planetą o średnicy dwukrotnie mniejszej od średnicy Ziemi. Jego masa stanowi 11% masy Ziemi. Obiega on Słońce w odległości średniej 1.52 j.a.
a) Jaki jest okres jego obiegu wokół Słońca ?
b) Wyznacz pierwszą prędkość kosmiczną dla tej planety
c) Jaką prędkość musiałby mieć statek kosmiczny na Marsie, aby móc powrócić na Ziemię ?
Zadanie 8. Wokół Słońca o masie M krąży po orbicie kołowej planeta o masie m. Jeżeli okres obiegu planety ma wartość T, to jak można obliczyć promień orbity planety R (określ zależność)
Zadanie 9. Wyznacz I i II prędkość kosmiczną dla planety o masie 2x większej od Ziemi, ale o tej samej objętości.
Zadanie 10.  Planeta o masie 6 • 10²⁴ kg działa na ciało o masie 200 g umieszczone na jej powierzchni w odległości 40• 10⁶ m od jej środka. Oblicz wartość siły oddziaływania ciała i tej pla­nety:

Zadanie 11.  Wokół Słońca o masie M krąży po orbicie kołowej planeta o masie m. Jeżeli okres obie­gu planety ma wartość T, to jak można obliczyć promień orbity planety R (określ zależność):

Zadanie 12.  Aby przesunąć ciało o masie 10 kg ruchem jednostajnym z punktu A o potencjale grawitacyjnym – 10 J/kg do punktu B, trzeba wykonać pracę 40 J. Oblicz wartość potencjału grawitacyjnego w punkcie B 
Zadanie 13. Dwa ciała o masach 30 kg oraz 50 kg są oddalone od siebie o  5 m. Wyznacz siłę oddziaływania ciał. Wykonaj rysunek oddziaływania.

Zadanie 14. Dwie jednakowe małe jednorodne kulki, każda o masie m=5 kg, umieszczono w odległości 10m. 

a)    narysuj wektor natężenia pola grawitacyjnego w odległości 8 m od pierwszej kulki
Wyznacz wartość natężenia pola grawitacyjnego wytworzonego przez układ kulek w  tym punkcie, znajdującym się w odległości 8 m od pierwszej kulki: 
Zadanie 15. Oblicz średnią gęstość planety Y, na której przyśpieszenie grawitacyjne wynosi  12 m/s². Promień planety  16·10⁶ m.

Zadanie 16. Po podróży na Marsa kolejną wyprawą kosmiczną ludzi może być misja na Wenus. Wiedząc, że masa Wenus wynosi 4·10²⁴ kg i promień  6·10⁶ m, oblicz, jaki ciężar będzie miał kosmonauta na Wenus, którego masa z oprzyrządowaniem wynosi  90 kg.

Zadanie 17. Odległość między środkiem Ziemi a środkiem Księżyca wynosi  380 000 km, masa Ziemi jest n = 81 razy większa od masy Księżyca. W jakiej odległości od środka Ziemi znajduje się punkt (na linii łączącej środki Ziemi i Księżyca), w którym siła przyciągania ku Ziemi jest równa sile przyciągania ku Księżycowi?

Zadanie 18. Promień Jowisza wynosi  71,35·10⁶ m. Jeden z księżyców Jowisza okrąża go po orbicie kołowej o promieniu   1,9 .10⁹ m w czasie  16,7 dnia ziemskiego. Przyjmując, że masa księżyca jest nieznaczna w porównaniu z masą Jowisza, oblicz przyśpieszenie grawitacyjne na powierzchni Jowisza.

Zadanie 19 Czarna dziura

„Czarna dziura” to ciało o olbrzymiej gęstości, to znaczy  ciało o bardzo dużej masie zajmujące bardzo małą objętość. Pole grawitacyjne czarnej dziury jest tak silne, że nic – nawet światło – nie może opuścić jej pola grawitacyjnego. Oblicz, ile wynosiłby promień ciała o masie równej masie Ziemi M = 6·10²⁴ kg, gdyby prędkość ucieczki z pola grawitacyjnego tego ciała (druga prędkość kosmiczna)  była równa prędkości światła  c = 300 000 km/s.

Zadanie 20. Manewry rakiety w Kosmosie

Pojazd rakietowy krąży naokoło Ziemi po orbicie kołowej o promieniu r = 2R, gdzie R jest promieniem Ziemi. Oblicz, ile razy mniejszą pracę muszą wykonać  silniki pojazdu, aby mógł on się wznieść na orbitę o promieniu równym 3R, w stosunku do pracy wyniesienia pojazdu na pierwszą orbitę.

Hydrostatyka i bilans cieplny

BILANS
Zadanie 1
Do wody o masie 0,4 kg i temperaturze 500C wrzucono kostkę lodu o masie 0,1 kg i temperaturze 0 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 2
W naczyniu znajduje się 0,5 kg lodu o temp. 0 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 3
Oblicz prędkość, jaką powinna mieć bryłka lodu o temp. -10 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cieplną.
Zadanie 4
Do wody o masie 0,8 kg i temperaturze 600C wrzucono kostkę lodu o masie 0,2 kg i temperaturze 0 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 5
W naczyniu znajduje się 0,5 kg lodu o temp. 0 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 6
Oblicz, z jakiej wysokości powinna upaść bryłka lodu o temp. -5 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cieplną.
Zadanie 7
W naczyniu znajduje się 1,5 kg lodu o temp. -5 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 8
Oblicz, z jakiej wysokości powinna upaść bryłka lodu o temp. 0 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cieplną.
Zadanie 9
Do wody o masie 0,3 kg i temperaturze 400C wrzucono kostkę lodu o masie 0,1 kg i temperaturze -5 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 10
Do wody o masie 0,5 kg i temperaturze 500C wrzucono kostkę lodu o masie 0,2 kg i temperaturze -10 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 11
Do wody o masie 0,4 kg i temperaturze 500C wrzucono kostkę lodu o masie 0,1 kg i temperaturze 0 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 12
W naczyniu znajduje się 0,5 kg lodu o temp. 0 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 13
Oblicz prędkość, jaką powinna mieć bryłka lodu o temp. -10 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cieplną.
Zadanie 14
Do wody o masie 0,8 kg i temperaturze 600C wrzucono kostkę lodu o masie 0,2 kg i temperaturze 0 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 15
W naczyniu znajduje się 0,5 kg lodu o temp. 0 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 16
Oblicz, z jakiej wysokości powinna upaść bryłka lodu o temp. -5 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cieplną.
Zadanie 17
W naczyniu znajduje się 1,5 kg lodu o temp. -5 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 18
Oblicz, z jakiej wysokości powinna upaść bryłka lodu o temp. 0 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cieplną.
Zadanie 19
Do wody o masie 0,3 kg i temperaturze 400C wrzucono kostkę lodu o masie 0,1 kg i temperaturze -5 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 20
Do wody o masie 0,5 kg i temperaturze 500C wrzucono kostkę lodu o masie 0,2 kg i temperaturze -10 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 21
Do wody o masie 0,4 kg i temperaturze 500C wrzucono kostkę lodu o masie 0,1 kg i temperaturze 0 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 22
W naczyniu znajduje się 0,5 kg lodu o temp. 0 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 23
Oblicz prędkość, jaką powinna mieć bryłka lodu o temp. -10 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cieplną.
Zadanie 24
Do wody o masie 0,8 kg i temperaturze 600C wrzucono kostkę lodu o masie 0,2 kg i temperaturze 0 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 25
W naczyniu znajduje się 0,5 kg lodu o temp. 0 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 26
Oblicz, z jakiej wysokości powinna upaść bryłka lodu o temp. -5 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cieplną.
Zadanie 27

W naczyniu znajduje się 1,5 kg lodu o temp. -5 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 28
Oblicz, z jakiej wysokości powinna upaść bryłka lodu o temp. 0 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cieplną.
Zadanie 29
Do wody o masie 0,3 kg i temperaturze 400C wrzucono kostkę lodu o masie 0,1 kg i temperaturze -5 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 30
Do wody o masie 0,5 kg i temperaturze 500C wrzucono kostkę lodu o masie 0,2 kg i temperaturze -10 0C. Oblicz temperaturę końcową mieszaniny.
Zadanie 31
W naczyniu znajduje się 0,5 kg lodu o temp. 0 0C. Oblicz, ile ciepła potrzeba dostarczyć, aby lód całkowicie zmienić w parę o temperaturze 100 0C
Zadanie 32
Oblicz, z jakiej wysokości powinna upaść bryłka lodu o temp. -5 0C, aby całkowicie mogła się stopić. Przyjmij że cała energia mechaniczna zamieniła się w energię cibilanseplną.


HYDROSTATYKA
1. Klocek drewniany o masie 0,4 kg zawieszony na siłomierzu zanurzono do połowy w wodzie. Jaką wartość siły wskazuje siłomierz? Gęstość wody 1000 kg/m3, a drewna 600 kg/m3.
2. Oblicz gęstość drewna, z którego wykonano klocek sześcienny, jeżeli po wrzuceniu go do nafty o gęstości 0,8 g/m3, pływa zanurzony do 4/5 swej wysokości.
3. Bryłkę metalu o objętości 100 cm3 zawieszono w powietrzu na siłomierzu, który wskazał 8 N. Jaka wartość wskaże siłomierz, gdy bryłkę zanurzymy w wodzie o gęstości 1000 kg/m3?
4. Jaka musi być co najmniej powierzchnia kry lodowej grubości 25 cm, aby uniosła człowieka o masie 70 kg? Gęstość lodu wynosi 920 kg/m3, a wody 1000 kg/m3.
5. Ile wynosi objętość góry lodowej pływającej w morzu, jeżeli wystająca część ma objętość 10000 m3? Gęstość lodu wynosi 920 kg/m3, a wody 1000 kg/m3.
6. Oblicz gęstość jednorodnego ciała, którego ciężar w powietrzu Qp = 2,8 N, a wodzie Qw = 1,8 N. Siłę wyporu powietrza pomijamy. Gęstość wody ρw = 1000 kg/m3.
7. Ciężar pewnego ciała zanurzonego w odzie jest n = 3 razy mniejszy od ciężaru tego ciała w powietrzu. Ile wynosi gęstość tego ciała?
8. Kawałek jednorodnego metalu zanurzony w wodzie waży Q1 = 0,79 N, a zanurzony w nafcie waży Q2 = 0,81 N. a) Jaka jest gęstość tego metalu? b) Jaką objętość ma kawałek metalu?
9. Kawałek stopu miedzi i cynku w powietrzu waży P = 0,16 N, a w wodzie Q = 0,14 N. Oblicz skład procentowy tego stopu (wagowo). Gęstość miedzi ρCu = 8960 kg/m3, zaś cynku ρZn = 7100 kg/m3.
10. Jednorodny sześcian pływa w rtęci, przy czym 1/5 części jego objętości jest zanurzona. Jeśli na nim postawimy drugi sześcian o takich samych wymiarach, to sześcian dolny zanurzy się do połowy swojej objętości. Znajdź gęstość drugiego sześcianu. Gęstość rtęci wynosi 13,6*103 kg/m3.
11. Probówka ze śrutem o masie 0,02 kg zanurza się w cieczy o gęstości 800 kg/m3 do pewnej głębokości. Po wrzuceniu do probówki ciężarka o masie 0,05kg zanurza się ona do tej samej głębokości w innej cieczy. Oblicz gęstość tej cieczy.
12. Na powierzchni morza dryfuje bryła lodu. Część tej bryły o V= 300m3 wystaje ponad poziom wody. Oblicz
a) V całej bryły
B) V zanurzonej części bryły d wody = 1030kg/m3 d lodu= 900kg/m3
13. Jeden koniec rurki w kształcie litery U jest zamknięty, a drugi otwarty. W rurce znajduje się rtęć, przy czym w zamkniętym ramieniu jest jej więcej o 1 cm. Jakie ciśnienie panuje w zamkniętej części rurki, jeśli ciśnienie atmosferyczne wynosi 770mmHg.
14. Do rurki w kształcie litery U wlano rtęć, a następnie dolano wody. Zmierzono, ze różnica poziomu cieczy w obu tych naczyniach wynosi 25cm. Oblicz h słupa wody. (drtęci = 13 600 kg/m3)
15. Jednorodny sześcian pływa w rtęci przy czym 1/5 części jego objętości jest zanurzona. Jeśli na nim postawimy drugi sześcian o takich samych wymiarach, to sześcian dolny zanurzy się do polowy swojej objętości. Znajdź gęstość drugiego sześcianu. Gęstość rtęci wynosi 13,6 * 10³ kg/m²